Dynamic heat transfer through a hollow block wall in a naturally ventilated dwelling

1. Introduction

Hollow blocks are extensively used for walls in dwelling constructions in many countries.

According to a report by Mordor Intelligence, (2023) the growth in the use of hollow concrete blocks will occur in all regions of the world, however, the Asia-Pacific region in countries such as China, India, Malaysia, or Singapore, among others, will experience the greatest growth, especially in the residential segment. In Mexico, it is the constructive system most used to build envelope walls in recent houses (Huelsz et al., 2011). Thus, it is important to understand and assess the thermal performance of this type of envelope wall constructive system in Mexican climates. Heat transfer through hollow block constructive systems involves two or three-dimensional conduction through the solid material, natural air convection inside the cavities, and radiation between air-cavity surfaces.

In Mexican climates the oscillation during the day is large and the solar radiation is high, thus the time-dependent or dynamical model for the heat transfer through walls must be used (Huelsz et al., 2014). The steady-state model is only helpful in estimating the heating needs in winter for countries in temperate or cold climates with low solar radiation and small temperature oscillation during the day compared with the difference between average outdoor and indoor temperatures (Kuehn et al., 2001). Nevertheless, most of the heat transfer studies through hollow block constructive systems for walls consider the steadystate model. Some of these studies analyzed the relative contribution of the three heat transfer mechanisms: conduction through the solid frame, and convection and radiation through the air cavities (Ait-taleb et al., 2008; Borbón et al., 2010). The relative importance varies depending on the hollow block geometry and the temperature difference between wall surfaces. The conduction contribution decreases while convection and radiation contributions increase as the temperature difference between wall surfaces increases (Ait-taleb et al., 2008).

Fewer studies use the time-dependent or dynamic model to evaluate the heat transfer of hollow block or brick walls. A pioneering work by Rao & Chandra, (1970) used an electrical resistance-capacitance (R-C) network analog method to account for two-dimensional heat transfer. These authors did not specify how they modeled the convective and radiative heat transfer inside the air cavities. Steady and periodic thermal characteristics of concrete hollow blocks were experimentally obtained from an R-C network analyzer (Rao & Dance, 1968). These characteristics were used to evaluate the thermal performance of concrete hollow block wall sections exposed to a typical summer sol-air temperature diurnal cycle under a tropical climate, for air-conditioned and non-air-conditioned situations, showing that the hollow block design with two large air cavities is not thermally efficient under this climate. Gao et al., (2004) and Sala et al., (2008) made hot box experiments and numerical simulations considering a fixed temperature in a chamber at one side of the wall, like in air-conditioned buildings, and a temperature change in a chamber at the other side. Gao et al., (2004) produced a linear step change of the air temperature within one chamber and developed a theoretical three-dimensional heat transfer model including the natural convection and radiation effects in air cavities using convective and radiative heat transfer coefficients. The heat rate through the wall was used to compare experimental and numerical results; slight discrepancies were attributed to imperfect adiabatic conditions in the laterals of the experimental wall. Sala et al., (2008) produced a triangular function change in the air temperature within one chamber. Using the measured outside and inside surface temperatures, the measured interior and exterior ambient temperatures, and the exterior and interior surface thermal resistances, obtained from previous experiments, they calculated the response factors of the hollow brick wall. They used finite volume software (Fluent) to numerically obtain the response factors, without specifying in their paper how they simulated the heat transfer mechanisms involved. The response factors obtained from experiments and simulations were similar. Vivancos et al., (2009) reported a model for the thermal characterization of hollow bricks based on experimental results from a guarded hot plate in steady and dynamic conditions. The characterization is given by the thermal resistance and two parameters that are related to the thermal diffusivity and geometric characteristics of the brick. Other two papers proposed models for the dynamic heat transfer through hollow block walls. Zhang & Wachenfeldt, (2009) proposed one-layer and two-layer one-dimensional models with equivalent thermal conductivity and mass density to represent the effect of concrete walls with air cavities. Nevertheless, these authors do not analyze the convection inside the cavities nor the radiation between its internal walls. Li et al., (2016) developed a simplified heat transfer model of hollow blocks by using the finite element method in the frequency domain considering the convection and radiation inside the cavities and deriving the Conduction Transfer Function (CFT) coefficients of a hollow block from the identified s-polynomial transfer function. They compared the predicted surface temperature at both sides of a hollow concrete block to that measured in experiments for time-period conditions. Huelsz et al., (2016) proposed the equivalent-homogenous-layer-set (EHLS) method, which considers the two-dimensional conduction through the solid, natural convection inside air-cavities and radiation between air-cavity surfaces. The method gives a thermal equivalent wall composed of at least three homogeneous layers with time-dependent properties, which can be implemented in whole-building simulation programs. They compared results with an experimentally validated two-dimensional model. The total thermal load difference is up to 6% for the air-conditioned room. For the non-air-conditioned room, the difference in the energy transferred through the wall is up to 3.4%, and the sol-air decrement factor and the lag-time have differences up to 7%. Barrios et al. (2017) implemented the EHLS method in whole-building simulations using Energy Plus and validated the simulations with experimental results from a whole year of measurements in a non-air-conditioned test hut constructed with hollow concrete block walls and a roof comprised of hollow concrete block and T-beams. Xamán et al. (2017) employing computational fluid dynamic (CFD) simulations studied the thermal performance of hollow blocks roof used in Mexico. They analyzed the effect of adding insulation and a reflective material coating on the external side of the roof. Huelsz et al., (2019) evaluated five heat transfer models for hollow blocks in whole-building energy simulations. Cherem-Pereira et al., (2020) proposed the coupling of building energy simulation software with CFD software to consider the three-dimensional time-dependent heat transfer through hollow blocks. The method can potentially increase the precision in the energy analysis of these elements, but due to the high computer run time, in their study, only one wall was modeled the others were considered adiabatic, and the simulations were limited to one day period. Jamal et al., (2021) performed two-dimensional CFD simulations to analyze the thermal performance of three hollow blocks submitted to sinusoidal heating on the outdoor side. They pointed out the importance of the emissivity of the internal surfaces on heat transfer. Chihab et al., (2021) employed two-dimensional CDF simulations of the steadystate heat transfer through two configurations of hollow block roofs to generate an equivalent homogeneous monolayer block. Using the equivalent model, they numerically solved the transient heat conduction equation under real conditions. They reported that convection and radiation within the cavities significantly impact the roof’s thermal behavior. Najjaoui et al., (2022) employing two-dimensional CDF simulations analyzed the heat transfer in a steady state through three configurations of hollow-block roofs considering the solar radiation effect. They showed that the blocks with a larger cavity height-to-length ratio have smaller heat transfer. (Hernández-Castillo et al., 2022) made three-dimensional CFD simulations to study the steady state convection and radiation heat transfer through the tall cavities formed in hollow-block walls. The effect of emissivity is analyzed, the radiative heat transfer represents more than 60% of the total heat transfer for emissivity 0.8, the common value for block materials. Nevertheless, with the extended research on hollow-block funds in the literature, none of these studies analyzed the relative importance of the three heat transfer mechanisms.

The term thermal bridge refers to the portion of a constructive system that transfers much more heat than other portions. In hollow blocks, the thermal bridge is referred to as the solid part of the hollow block (Antar, 2010), because in general, it is assumed that the solid portions of the hollow block, i.e. the framing path transfer much more heat than the air cavities, i.e. the in-cavity path (Kosny, 2004).

However, due to the increasing temperature difference between wall surfaces, there are increments in the convection and radiation heat transfer through the cavities (Ait-taleb et al., 2008), so it could be possible that the heat transfer through the in-cavity path is like that of the framing path, or even that the in-cavity path turns into the thermal bridge instead of the framing path. However, due to the increasing temperature difference between wall surfaces, there are increments in the convection and radiation heat transfer through the (Ait-taleb et al., 2008), so it could be possible that the heat transfer through the in-cavity path is similar to that of the framing path, or even that the in-cavity path turns into the thermal bridge instead of the framing path. No studies have been found that analyze this subject, thus the aim of the present study is to elucidate if for hot-dry climatic outdoor conditions and for a non-air conditioned indoor, the frame path is the main path for the heat transfer or not.

The present work reports surface temperature measurements of an envelope wall made of concrete hollow blocks of a non-air-conditioned house in a hot-dry climate, where the temperature difference between wall surfaces is considerable. The results are analyzed to study the relative importance of the heat transferred through the in-cavity path (hollow part) of the hollow block wall with respect to that transferred through the framing path (solid part).

The paper is structured as follows: Section 2 presents the methodology and Section 3 shows the results. The conclusion is pointed out in Section 4.

2. Methodology

This section presents the methodology used for the experiments and the analysis of the result.

2.1. EXPERIMENTS

The measurements were conducted in a concrete hollow block wall of a non-air-conditioned house in a hot-dry desert climate location. The house is constructed in Hermosillo, the capital of the state of Sonora. This city is in the North-Western zone of Mexico, 275 km south of the U.S. border and 2037 km from Mexico City, at 29° 05’ North latitude. High solar radiation levels, clear skies, and daily and annual high-temperature swings are typical of the local climate. The maximum air temperature exceeds 38°C on an average of 90 days of the year, including most days from early June until early September, with minimum air temperatures of 20-25°C and a maximum of about 40-44°C. Winters are comfortable, with minimum temperatures of 4-7°C and maximum between 25 and 30°C. The city has almost 300 sunny days per year; in spring and summer, solar radiation can rise up to 1000 W/m² (LEMA, 2014; Meteotest, 2008; Regents of the University of California, 2014).

The house, shown in Figure 1, corresponds to the most repetitive pattern of housing, which has an area of 45 m², known as “minimum housing,” and has a South-North orientation. The roof system consists of precast beams and polystyrene panels that are a framework for a thin layer of reinforced concrete on top. As a final finish, the roof has a waterproof membrane of white elastomeric polymer with high solar reflectance. All walls are made of 12 cm thick concrete hollow blocks, finished inside with white latex paint and outside with light brown acrylic wall putty with a solar absorptance of 0.4. Figure 2 presents an image and a sketch of the hollow concrete block.

Figure 1

The house, showing the main facade (South wall) used for the measurements

Figure 2

Concrete hollow block. (a) Image and (b) section with the dimensions, and units in meters

The outdoor and indoor surface temperature measurements were carried out on the main façade wall, South oriented, using temperature sensors. These measurements were carried out on June 10-15, August 28-31, September 3-11, and October 20-31, 2011. Four Onset TMC20-HD sensors were used, each connected to a HOBO U10 Data Logger; data were recorded every 10 minutes. Each temperature sensor was set into a small slot on the wall using a thermally conductive paste to ensure thermal contact. Two of the surface temperature sensors were placed on the indoor side of the wall, one corresponding to the center of a hollow, i.e., the center of an in-cavity path, and the other corresponding to the center of a solid part, i.e., the center of a frame path (see Fig. 3). The other two were set at the same locations of the outdoor side of the wall; the outdoor sensors were shielded from solar radiation using a ventilated aluminum sheet protection (see Fig. 4). The temperature sensors had an uncertainty of 0.1^oC.

Figure 3

Location of the indoor surface temperature sensors

Figure 4

Location of the outdoor surface temperature sensors with an aluminum solar shield

To precisely locate the surface temperature sensors at the center of the hollow and at the center solid part, an infrared camera was used to detect the surface temperature differences and locate the center of each part of the block (see Fig. 5).

Figure 5

Thermography of the south façade, where the center of the hollow part (H) and the center of the solid part (S) of the blocks can be located

2.2. ANALYSIS

The relative importance of the heat transferred through the in-cavity path (hollow part- H) of the hollow block wall respect to that transferred through the framing path (solid part-S) was calculated using the following methodology.

The heat transferred by unit area at any part of the outdoor surface of the wall, q_o, is given by

(1)

$q_o=h_o\left(T_{sa1}-T_{so}\right),$

where h_o is the heat transfer coefficient at the outdoor, T_sa is the sol-air temperature and T_so is the temperature at the outdoor surface of the wall.

The sol-air temperature is an equivalent temperature for the outdoor that considers the heat transfer at the outdoor side of the wall by convection and radiation; it is expressed as

(2)

$T_{sa}=T_a+\frac{A1}{h_o}+CF,$

where T_a is the outdoor air temperature, A is the solar absorptance of the outdoor wall surface, I is the solar radiation incident on the outdoor wall surface, and CF is the correction factor for the longwave radiation; it is taken as CF=0 for vertical walls (American Society of Heating Refrigerating and Air-Conditioning Engineers, 2009).

Meteorological data were obtained from the Meteorology station of the Energy, Environment and Architecture Laboratory (LEMA, 2014); the solar radiation incident on the outdoor wall surface was calculated from horizontal solar radiation and diffuse solar radiation data using transformation equations given by (Duffie & Beckman, 2013).

The ratio of the heat transferred through the in-cavity path to that transferred through the frame path at the outdoor surface, r_o, is given by

(3)

${\gamma }_o=\frac{q_{oH}}{q_{oS}}=\frac{h_o\left(T_{sa}-T_{soH}\right)}{h_o\left(T_{sa}-T_{soS}\right)}=\frac{T_{sa}-T_{soH}}{T_{sa}-T_{soS}},$

where q_oH and q_oS are the heat transferred by unit area through the in-cavity path and through the frame path at the outdoor surface, and T_soH and T_soS are the temperature at the wall outdoor surface measured at the center of the in-cavity path and at the center of the frame path, as shown in Fig. 6. Note that h_o has the same value for both H and S positions, thus it can be eliminated in equation (3).

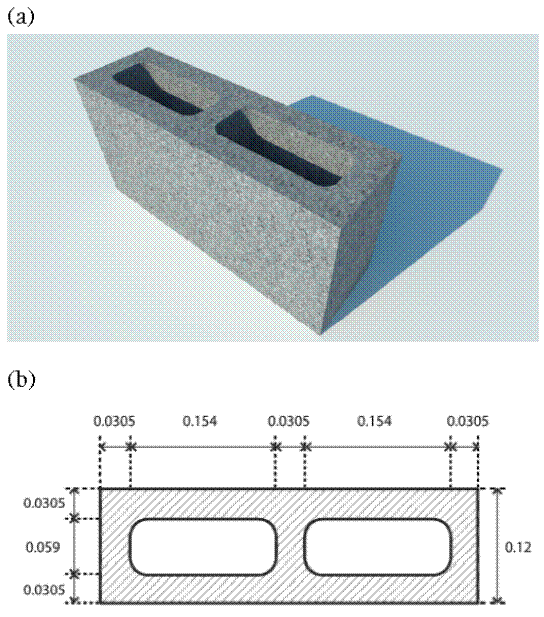
Figure 6

Horizontal section of the wall, where the placement of the sensors in the hollow (H) and the solid (S) part of the block can be seen, both outside and inside

Similarly, the heat transferred by unit area at any part of the indoor surface of the wall, q_i, is given by

(4)

$q_i=h_i\left(T_{si}-T_i\right),$

where h_i is the heat transfer coefficient at the indoor, T_si is the temperature at the indoor surface of the wall and T_i is the indoor air temperature.

The ratio of the heat transferred through the in-cavity path to that transferred through the frame path at the indoor surface, r_i, is given by

(5)

$r_i=\frac{q_{iH}}{q_{iS}}=\frac{h_i\left(T_{siH}-T_i\right)}{h_i\left(T_{siS}-T_i\right)}=\frac{T_{siH}-T_i}{T_{siS}-T_i},$

where q_iH and q_iS are the heat transferred by unit area through the in-cavity path and through the frame path at the indoor surface, and T_siH and T_siS are the temperature at the wall indoor surface measured at the center of the in-cavity path and at the center of the frame path, as shown in Fig. 6. Also, hi has the same value for both H and S positions, thus it can be eliminated in equation (5).

The relative importance of the heat transferred through the in-cavity path (hollow part-H) of the hollow block wall with respect to that transferred through the framing path (solid part-S) is estimated by of r_o and r_i. It is worth mentioning, that r_o and r_i could be calculated directly by using heat flux meters at the same points where the temperatures were recorded, nevertheless, the authors did not get the sensors on time while they had access to the house.

3. Results

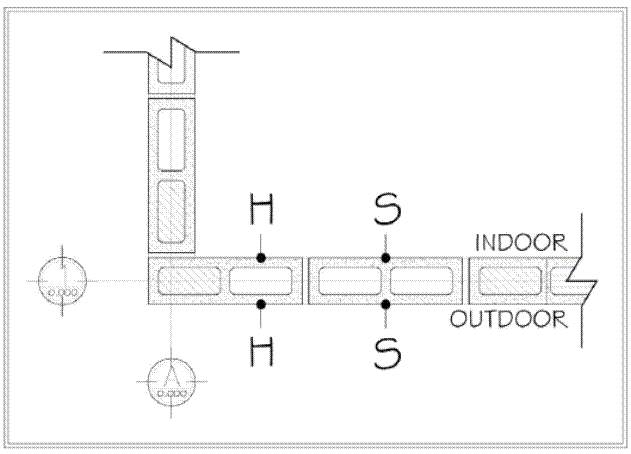
As an example, the surface temperatures measured by the four sensors during four days in August are shown in Figure 7. The outdoor air temperature, the indoor air temperature, the sol-air temperature, and the total horizontal solar radiation are included. It can be observed the typical climatic conditions of a hot-dry climate, high solar radiation (near 1000 W/m² at noon) and large oscillation amplitudes of the outdoor air temperature (larger than 13^oC) and the sol-air temperature (larger than 24^oC). The temperature difference between indoors and outdoors is up to 8ºC before sunrise. Also, it can be observed that as expected the oscillation amplitudes of the indoor surface temperatures are smaller than that of the outdoor surface, also there is a time lag of the indoor surface temperatures with respect to the outdoor ones. On the same side of the block, slight differences between the temperatures of both parts of the block can be appreciated.

Figure 7

Surface temperatures on the indoor side (Tsi) and on the outdoor side (Tso) for hollow, H, and solid, S, parts of the block. Outdoor air temperature (To), indoor air temperature (Ti), sol-air temperature (Tsa), and horizontal solar radiation (R), as a function of civil time

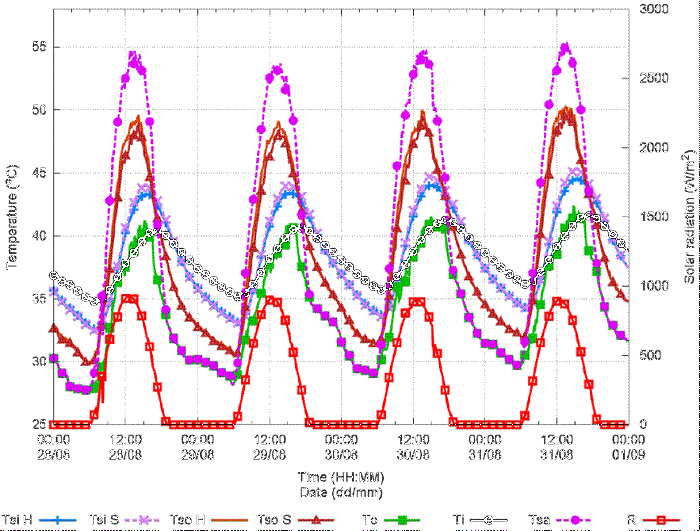
Figure 8 presents q_o / h_o = (T_sa -T_so) as a function of time for the same four days of Figure 7, horizontal solar radiation is included as a reference. It can be observed that heat is transferred from the wall surface to the outdoor air during the night, while during the daytime the heat is transferred from the outdoor air and solar radiation to the wall surface.

Figure 8

Difference of the sol-air temperature and the outdoor surface temperature, Tsa-Tso, as a function of civil time. Horizontal solar radiation, R, is plotted as reference

Figure 9 shows q_i/ h_i = (T_si- T_i) as a function of time for the same four days. It can be observed that the heat transferred through the indoor wall surface has a time lag with respect to that transferred through the outdoor surface (Figure 8). From about 21:00 to 10:00 hours the heat is transferred from the indoor air to the wall, while from 10:00 to 21:00 hours the heat is transferred from the wall to the indoor air.

Figure 9

Difference of the indoor surface temperature and the indoor air temperature, Tsi-Ti, as a function of civil time. Horizontal solar radiation R is plotted as reference.

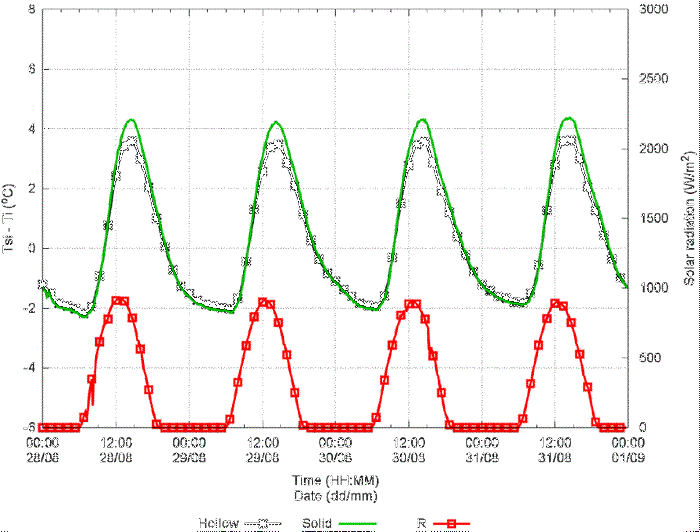
Figure 10 presents r_o as a function of time for the same four days. As can be observed that during the night, r_o is around one, thus the heat transferred though the in-cavity path is practically the same of that transferred through the frame path. Thus, during the night, the frame path does not represent a thermal bridge. During most of the daytime, r_o is greater than 0.7, thus although the frame path transfers more heat than the in-cavity path, it cannot be considered as a thermal bridge. Close to the sunrise and sunset, the direction of the transference of heat at one path is inverted and r_o reaches low or high values.

Figure 10

Ratio of the heat transferred through the in-cavity path (hollow part-H) to that transferred through the frame path (solid part-S) for the outdoor surface, r_o, as a function of time. Horizontal solar radiation, R, is plotted as a reference

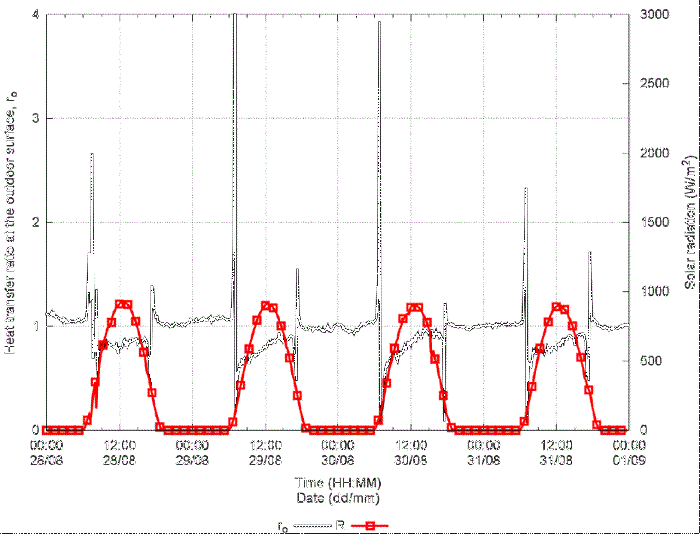
This last means that the thermal bridge is the in-cavity path for short periods. The chute-down of the curve occurs when the heat transfer at the in-cavity path changes direction, while the piqueup occurs when the heat transfer in the frame path changes direction.

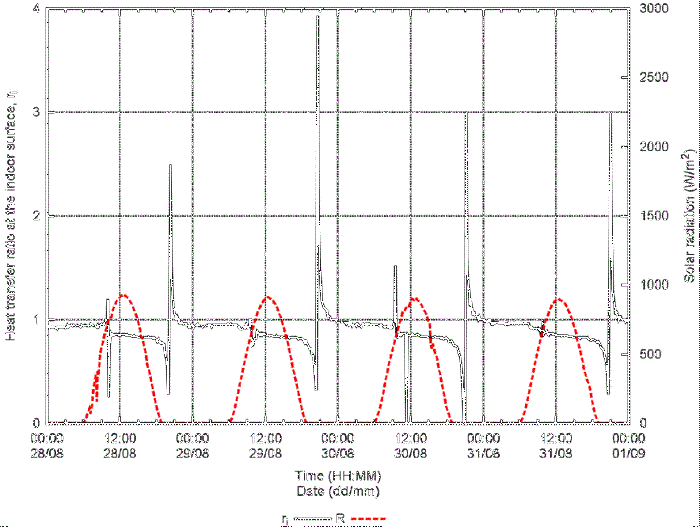
Figure 11 shows the ratio of the heat transferred through the in-cavity path (hollow part-H) to that transferred through the frame path (solid part-S) for the indoor surface, r_i, as a function of time. Most of the time r_i is greater than 0.7 and lower than 1.0, confirming that the frame path cannot be considered a thermal bridge. There are also short periods where the thermal bridge is the in-cavity path.

Figure 11

Ratio of the heat transferred through the in-cavity path (hollow part-H) to that transferred through the frame path (solid part-S) for the indoor surface, r_i, as a function of time. Horizontal solar radiation, R, is plotted as reference

The results for all measurements periods are like that shown in previous figures. Not considering the short time intervals when the direction of the transference of heat at one path is inverted at one side of the wall, implying that r_o or r_i reaches a low or high value, the average and standard deviation of r_o and r_i are taken and they are reported in Table 1. The uncertainties associated to r_o and to r_i due to the uncertainty of temperature measurements are smaller than the respective standard deviation. As can be observed, for the four periods of measurements, r_o and r_i are close to one, which shows that the heat transferred through both paths is similar. This result is obtained in a wall of a non-air-conditioned house in a hotdry climate characterized by high solar radiation, large oscillation amplitude of the outdoor air temperature, high values of the wall sol-air temperature, and high-temperature difference between wall outdoor and indoor surfaces, conditions that promote the increase of convection and radiation heat transfer through the hollow block air cavities (del Coz Díaz et al., 2011).

The averages and standard deviations of the daily horizontal solar radiation maximum, R_max, of outdoor air temperature amplitude, ΔT_a, of the sol-air temperature maximum, of the sol-air temperature maximum, T_sa-max, and of the maximum difference between wall outdoor and indoor surfaces temperatures, ${\left|T_{so}-T_{si}\right|}_{max}$, are also reported in Table 1.

5. Conclusions

Dynamic heat transfer through the constructive system of a house plays an important role in thermal performance. Hollow concrete blocks are extensively used alone or as a part of a more complex construction system. Heat transfer through hollow concrete blocks includes conduction in two or three dimensions, convection, and radiation through the air cavities. It has been reported that thermal bridges are found in the solid part, also known as the framing path, of the hollow concrete blocks.

Wall surface temperature measurements in a non-air-conditioned house in a hot-dry climate were made to study the heat transfer through the framing part (solid part) and the in-cavity path (hollow part) during four time periods from June to October 2011, (more than 30 days).

The heat transferred through the frame path and through the in-cavity path inside the house are similar. The ratio of heat transferred through the frame path r_i is slightly different during the night than during the day except for moments when the direction of the heat transfer of one path is inverted, so the other path can be considered the thermal bridge. At night, the in-cavity path transfers almost the same heat as the frame path; during the day, the in-cavity path transfers 0.7 of the heat transferred by the frame path. Thus, it is concluded that the frame path cannot be considered by default as a thermal bridge and the in-cavity path as the low heat transfer portion.

The conclusion of this work for a hollow concrete block used in a non-air-conditioned house in a hot-dry climate is that there is no thermal bridge and further research must be done for other hollow block geometries and materials. Understanding the heat transfer mechanisms involved in the thermal behavior of a hollow concrete block wall in a hot-dry climate will allow the generation of methods and guidelines for designers and builders. This will facilitate the selection of hollow blocks for envelope walls according to the climate and the use or not of air conditioning systems.